Steady-state dynamics and nonlocal correlations in thermoelectric Cooper pair splitters
Arnav Arora, Siddhant Midha, Alexander Zyuzin, Pertti Hakonen, and 1 more author
npj Quantum Information, Mar 2025
Publisher: Nature Publishing Group
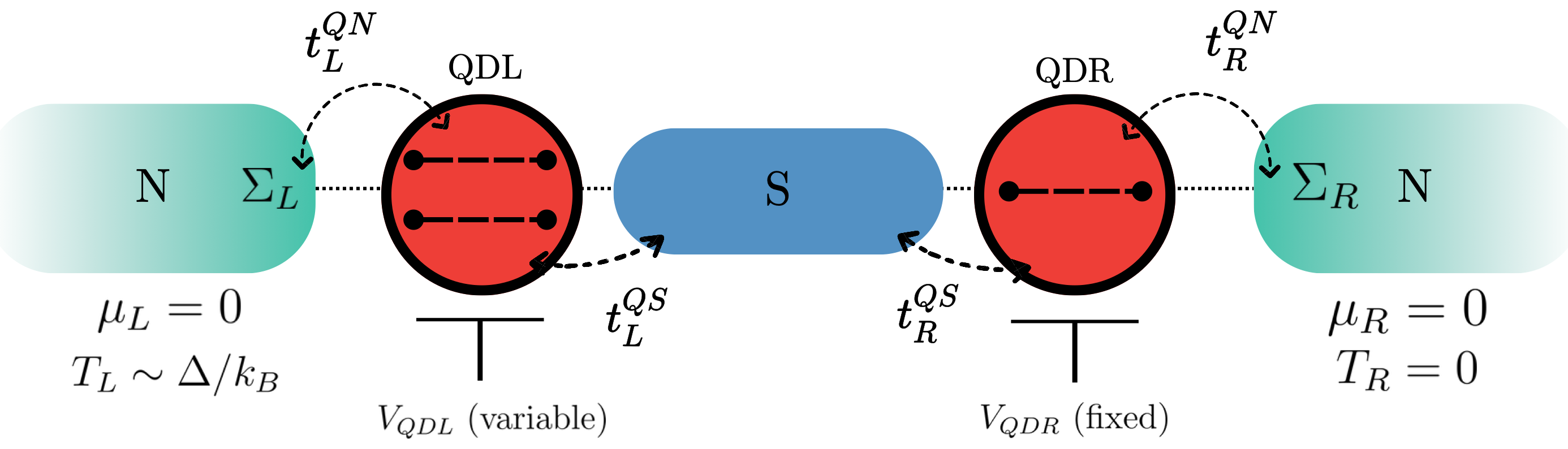
Recent experiments on Cooper pair splitters using superconductor-quantum dot hybrids have embarked on creating entanglement in the solid-state, by engineering the sub-gap processes in the superconducting region. Using the thermoelectric Cooper pair splitter setup [Nat. Comm., 12, 21, (2021)] as a prototype, we present a comprehensive analysis of the fundamental components of the observed transport signal, aiming to critically clarify the operating regimes and confirm the nonlocal and nonclassical nature of correlations arising from crossed Andreev processes. By making a nexus with quantum discord, we identify operating points of nonlocal quantum correlations in the CPS device—information that cannot be extracted from the transport signal alone. A notable consequence of our analysis is the finding that contact-induced level broadening of the quantum dot’s discrete energy spectrum, along with its hybridization with the superconducting segment, can lead to shifted resonances in the crossed Andreev process as well as a parity reversal in the thermoelectric current. Our work thereby provides detailed insights into the gate voltage control of the quantum correlations in superconducting-hybrid Cooper pair splitters, revealing new avenues for harnessing quantum correlations in solid-state systems.
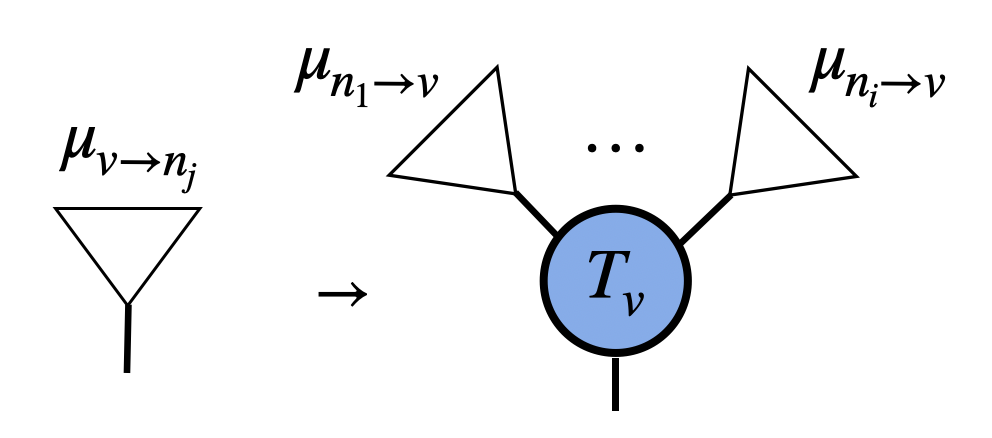 Beyond Belief Propagation: Cluster-Corrected Tensor Network Contraction with Exponential ConvergencearXiv preprint arXiv:2510.02290, Mar 2025
Beyond Belief Propagation: Cluster-Corrected Tensor Network Contraction with Exponential ConvergencearXiv preprint arXiv:2510.02290, Mar 2025